Text indexing in python - mapping text to values using finite-state transducers
In the previous posts I wrote about the finite-state automata (FSA) - data structures that could store a set of words. Sets are quite useful, but not nearly as useful as dictionaries. Luckily for us we can quite easily extend the implementation of FSA and allow it to also store the mapping from the words to values. Such data structures are called finite-state transducers (FST).
In the post I will focus on storing the natural numbers as they can be in turn used as an index to the array which can store any type of value, but storing e.g. strings is also a viable option. The algorithm presented below was published by Mihov and Maurel[1] and adapted to store integers. If you haven’t read the previous post I highly encourage it as this post will be building upon the foundations laid out there.
The base idea is to take the finite-state automaton and add a single value to each transition (edge), and a list of values to a state (node). The value (or values) the word maps to can be retrieved by following the transitions indexed by the consecutive letters of the word and summing up values on the edges along the way, and then adding them to the values in the final node. Let’s take a look at the example:
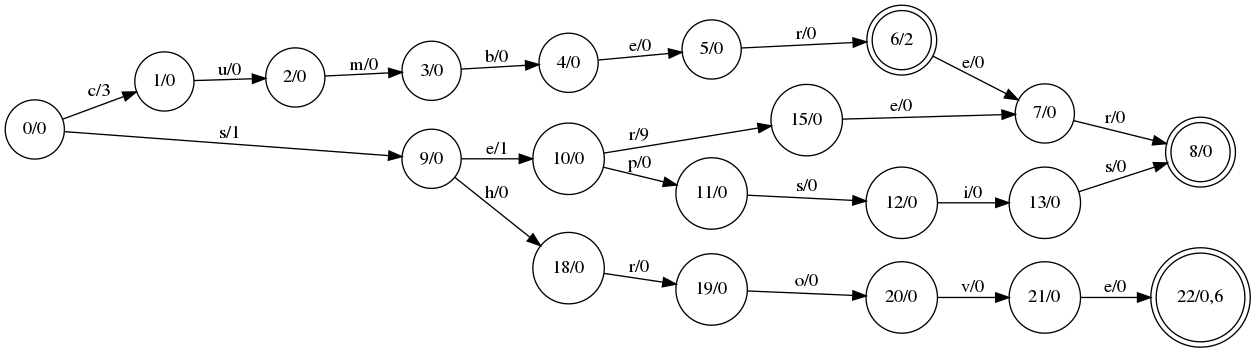
What’s the value of the “cumber” word? It’s value on the s0->s1 edge (3) plus value on the node s6 (2) which equals to 5. “cumberer” value is s0->s1 edge value (3) plus final node value (0) which equals to 3. “shrove” has two values stored - 1 and 7. The value of the word “sepsis” is 2 and the value of the word “serer” is 11.
One important thing to note now is that there seems to be many possibilities in which you could put e.g the value 3 on the “cumber” path. In this case the result would be the same if it was put on the s1->s2 edge or s2->s3 edge and so on. Why did we decide to put it on the s0->s1 edge? We want to put the values as close to the starting node as possible. If we didn’t do this we could create a situation where we cannot minimize the suffixes because of the values stored there. This allows us to build the smallest automaton.
Hopefully this gives and idea how the vales can be stored using the automaton. Now let’s see some code.
Updated State code
First let’s take a look at the State subclass code:
class MultiValueState(State):
def __init__(self, label):
super().__init__(label)
self.value = set([0])
def add_transition_to_a_new_state(self, c, label, value=0):
s = self.new(label)
self.add_transition(c, (s, value))
return s
def add_suffix(self, word, labels):
state = self
for c in word:
state = state.add_transition_to_a_new_state(c, next(labels))
state.final = True
return state
def next_state(self, c):
x = self.next_state_with_value(c)
if x is not None:
return x[0]
else:
return None
def next_state_with_value(self, c):
return self.transitions.get(c, None)
def set_state_value(self, value):
self.value = value
def get_word_value(self, w):
s = self
t_v = 0
for c in w:
s, v = s.next_state_with_value(c)
t_v += v
if s is None:
return []
if s.final:
return [d + t_v for d in s.value]
else:
return []
The changes mostly have to do with storing pairs of (State, int) instead of just State in the transition dictionary. Exception is get_word_value method - it gets the values encoded in the automation for a given word w.
Equivalency of the FST nodes
If you remember from the previous post an important part of the algorithm building the FSA was replacing the new nodes with their equivalents already present in the automaton to get the minimal possible version of it. It’s the same in the case of FST. Below you’ll find an updated replace_and_register method which aim is to minimize the last added word. The change from before is the need to preserve the value stored on the edge when you’re pointing it to an equivalent node. The first and last line of the method were modified to accomplish that:
def replace_or_register(state, register):
last_c, (last_child, value) = state.last_transition()
if last_child.transitions:
replace_or_register(last_child, register)
eq_state = register.get(last_child)
if eq_state is None:
register.put(last_child)
else:
state.add_transition(last_c, (eq_state, value))
Next we need to update our definition of equivalency as our definition of states changed. Now they are storing some values. Before we stated the states are equivalent if:
- they are both final or both non-final,
- their transitions have the same labels and lead to equivalent states.
In addition to the points above we’ll add the following conditions:
- the values stored on the states are the same,
- the transitions have the same values stored on them.
To accommodate for these changes we need to update our definition of key method, which is used in the state register to provide hashable key for a given state.
def key_obj_multi(state):
l = [state.final]
if state.final:
l += sorted(state.value)
for k, (s, v) in sorted(state.transitions.items(), key=lambda x: x[0]):
l.extend([k, id(s), v])
return tuple(l)
The algorithm
It’s now the time to take a look at the algorithm which builds the automaton. I put some comments inside which hopefully will be enough to explain the reasoning behind the code.
def minimal_fst_from_words(word_value_pairs):
# setting up the register with the new 'key' method
register = Register(key_obj_multi)
labels = inf_labels()
start_state = MultiValueState(next(labels))
prev_word = None
for word, word_value in word_value_pairs:
if prev_word is not None:
assert prev_word <= word
# here we do exactly the same thing we did when building FSA
last_state, pref_idx = common_prefix(start_state, word)
if last_state.transitions:
replace_or_register(last_state, register)
last_added = last_state.add_suffix(word[pref_idx:], labels)
# here starts the part responsible for handling the values
prev_state = start_state
stored_value = word_value
# here we manage the values on the common part of the last added word
# and currently added word
# we try to update the values so they're correct with the new word present
# and to keep them as close to the start state as possible
for j in range(pref_idx):
current_state, current_state_value = \
prev_state.next_state_with_value(word[j])
# we take the min of currently stored value and the value we want
# to store on the path, and we store it in the current transition
common_value = min(current_state_value, stored_value)
prev_state.add_transition(word[j], (current_state, common_value))
# we compute the remainder and push it downstream to all the
# transitions
push_next_value = current_state_value - common_value
for c, (s, v) in list(current_state.transitions.items()):
current_state.add_transition(c, (s, push_next_value + v))
# if we're in the final state we store the remainder value on it
if current_state.final:
current_state.set_state_value(
set([d + push_next_value for d in current_state.value])
)
# we compute the value we still need to store on our path in
# the downstram transitions
stored_value = stored_value - common_value
prev_state = current_state
#assert current_state should be just before last state
last_idx = pref_idx
if prev_word == word:
# if we have word repetition just store extra value on the last state
last_added.value.add(stored_value)
elif prev_state.transitions:
# otheriwse store the remainder just after the common prefix
current_state, current_state_value = \
prev_state.next_state_with_value(word[last_idx])
prev_state.add_transition(
word[last_idx],
(current_state, stored_value)
)
prev_word = word
replace_or_register(start_state, register)
return start_state, register
I hope you enjoyed reading the article. If you would like to contact me regarding the post drop me an email at: tostr.pl [at] gmail.com