Text indexing in Python with minimal finite-state automata
Have you ever wondered how Lucene/Elasticsearch does its job so well? This post will teach you about essential part of the Lucene index - minimal finite-state automaton (FSA), which allows for memory-efficient indexing of text. In the post you’ll find:
-
a few words about finite-state automata with a simple implementation in Python ,
-
introduction to constructing minimal automata containing:
On finite-state automata
Finite-state automata are data structures, which can recognize (sometimes infinite) set of words over some alphabet - we call this set a language. In essence they can do the same job as any set data structure available in your programming language or library of choice. They are particularly interesting because the representation they use is very memory efficient and allows to recognize the word of length m in O(m) time, which is not bad considering the compact representation.
Typical automaton is defined by five components: its states (like nodes in a graph), which incorporate a starting state and all end states, transitions between states (edges) and the alphabet.
Let’s look at the example. Here we have an automaton that stores the “wasp” and “wisp” words:
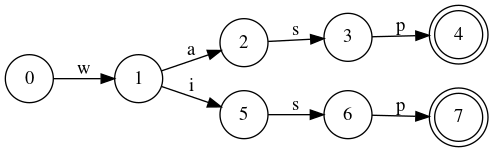
The circles are the states of the automaton. State 0 is the starting state and states 4 and 7 are the end states. Arrows indicate transitions and are labeled by the letters of the alphabet. If you can go from starting state to one of the end states only through transitions labeled by consecutive letters of the word, the word is in the language (set). Otherwise it isn’t. In the world of automata, we say that the word is accepted by the automaton.
This example hints slightly on the previously mentioned features of the FSA:
- retrieving word of length
mtakesO(m)as you need to go throughmtransitions to know whether word is in the set represented by FSA, - representation is compact as words may share states and/or transitions which encode them, here the transition
0->1and states 0 and 1 are shared and you learn later that they can actually share a lot more.
A simple implementation of such automaton might look like this:
class State(object):
def __init__(self, label):
self.label = label
self.transitions = {}
self.final = False
def next_state(self, c):
return self.transitions.get(c, None)
def accepts(self, w):
s = self
for c in w:
s = s.next_state(c)
if s is None:
return False
return s.final
def add_transition(self, c, s):
self.transitions[c] = s
def add_transition_to_a_new_state(self, c, label):
s = State(label)
self.add_transition(c, s)
return s
def set_final(self, final):
self.final = final
Let’s create the states and transitions:
s0 = State(0)
s1 = s0.add_transition_to_a_new_state('w', 1)
s2 = s1.add_transition_to_a_new_state('a', 2)
s3 = s2.add_transition_to_a_new_state('s', 3)
s4 = s3.add_transition_to_a_new_state('p', 4)
s4.set_final(True)
s5 = s1.add_transition_to_a_new_state('i', 5)
s6 = s5.add_transition_to_a_new_state('s', 6)
s7 = s6.add_transition_to_a_new_state('p', 7)
s7.set_final(True)
Now we can check that our automaton accepts the words “wasp” and “wisp”, and that it does not accept e.g “was” or “cat” by simply calling:
s0.accepts('was') // False
s0.accepts('wasp') // True
s0.accepts('wisp') // True
s0.accepts('cat') // False
It’s not very convenient to construct automata by hand, so let’s define a few methods to add words to automaton. Let’s look at the previous example to come up with a method to do it. First when adding a word “wasp” we just created a chain of transitions and marked last state as final. When adding “wisp” we found common prefix with existing words in automaton - “w” and state associated with it - s1 and then again added a chain of transitions to s1 through the remaining characters - “isp” suffix. Here’s the code implementing this algorithm:
def inf_labels(s=0):
while True:
yield s
s += 1
def add_suffix(state, word, labels):
for c in word:
state = state.add_transition_to_a_new_state(c, next(labels))
state.final = True
def common_prefix(state, word):
current_state = state
for i, c in enumerate(word):
s = current_state.next_state(c)
if s is not None:
current_state = s
else:
return current_state, i
return current_state, i + 1
def add_word(state, word, labels):
s_to_add, word_idx = common_prefix(state, word)
add_suffix(s_to_add, word[word_idx:], labels)
def trie_from_words(words):
labels = inf_labels()
s0 = State(next(labels))
for word in words:
add_word(s0, word, labels)
return s0
Calling the method trie_from_words like this trie_from_words(['wasp', 'wisp']) will construct the same automaton as the one specified by hand earlier. The resulting data structure is also called a trie, thus the name of the method.
Now it seems that our work is over. We have a method to construct an automaton from the given set of words and we can check if they’re encoded by the automaton. There is one problem though. This automaton for sure is not the best in terms of memory efficiency. It has some unnecessary states. Here is something more frugal but equivalent in encoded language:
s0 = State(0)
s1 = s0.add_transition_to_a_new_state('w', 1)
s2 = s1.add_transition_to_a_new_state('a', 2)
s3 = s2.add_transition_to_a_new_state('s', 3)
s4 = s3.add_transition_to_a_new_state('p', 4)
s4.set_final(True)
s1.add_transition('i', s2) # here we just add the new transition through 'i' from s1 to s2
It’ll look like this:

As you can see it reuses all the states from the “wasp” word and adds only one extra transition, which allows it to go through “i” from s1 to s2 to encode “wisp”. The effect is the same as before and we did it without 3 states!
The 2nd automaton has a very important property - it’s a minimal automaton accepting the language: ['wasp', 'wisp'], and because the memory efficiency is something we’re very interested in, we’ll try to find a method to construct such automaton for any given language.
Constructing minimal automata
State equality
First let’s think how we could transform the first automaton into the second one? We need to replace state s5 (and remove s6, s7) by already existing s2 state. We can say that s5 and s2 are equal in the sense that we can substitute one with the other without changing the language represented by the automaton. So how can we tell that the states are equal? Well it’s enough that the sets of the words which are encoded by the automaton starting in these states are equal [1]. Let’s make a method which generates a language represented by automaton starting in some state:
def get_lang(s0):
def _get_lang(s, w, lang):
if s.final:
lang.append(w)
for c, cs in s.transitions.items():
_get_lang(cs, w + c, lang)
lang = []
_get_lang(s0, '', lang)
return lang
This method traverses recursively all the states and transitions accessible from a given state, and adds the currently constructed word to a list when it reaches the final state. You can check that for the both automata from before it will output:
['wasp', 'wisp']
If you would try to call this method on states s2 and s5 from the 1st automaton you’ll get the same output ['sp'], which means that these can be substituted. Because of that we can resign from using the s5 altogether and just point states which would use it to s2.
Minimizing existing automata
We could minimize the first automaton by processing its states. When processing a state we would check if any of it’s children is equivalent to a state we already visited in the automaton, if we found such a state we would replace the child with it, if not we would put the child in the register for visited (and unique) states.
The register could be a simple object with dictionary and a method which can compute a hashable key for each state. The method should return the same key for equivalent states.
class Register(object):
def __init__(self, key):
self.key = key
self.states = {}
def get(self, state):
return self.states.get(self.key(state), None)
def put(self, state):
self.states[self.key(state)] = state
Now let’s define the method which would get us a key of the state for the register:
def key_lang(state):
return tuple(sorted(get_lang(state)))
It’s simply a sorted tuple containing the language encoded by an automaton starting in a given state - if the languages are equal the states are equal too.
Now let’s process the automaton. We will do it using post-order method (visit all the children first and then process the state).
def minimize_automaton(state, register):
for s in state.transitions.values():
minimize_automaton(s, register)
old_transitions = list(state.transitions.items())
print('Processing node:', state.label, register.key(state))
for c, s in old_transitions:
eq_state = register.get(s)
print(' Transition:', c)
if eq_state is None:
print(' Registering: ', s.label, register.key(s))
register.put(s)
else:
print(' Replacing', s.label, register.key(s), 'with', eq_state.label, register.key(eq_state))
state.add_transition(c, eq_state)
Calling it:
register = Register(key_lang)
minimize_automaton(s0, register)
will output the following and minimize automaton from 8 to 5 states:
Processing node: 4 ('',)
Processing node: 3 ('p',)
Transition: p
Registering: 4 ('',)
Processing node: 2 ('sp',)
Transition: s
Registering: 3 ('p',)
Processing node: 7 ('',)
Processing node: 6 ('p',)
Transition: p
Replacing 7 ('',) with 4 ('',)
Processing node: 5 ('sp',)
Transition: s
Replacing 6 ('p',) with 3 ('p',)
Processing node: 1 ('asp', 'isp')
Transition: a
Registering: 2 ('sp',)
Transition: i
Replacing 5 ('sp',) with 2 ('sp',)
Processing node: 0 ('wasp', 'wisp')
Transition: w
Registering: 1 ('asp', 'isp')
The presented solution works, but it has some weak points:
- Firstly, computing the language represented by state requires visiting all states reachable from it, which is ineffective.
- Secondly, the language encoded by an automaton will usually take a much more memory than the automaton itself, so using it as a key misses the point totally.
Luckily we can check state equivalence differently. States are equal if:
- they are both final or both non-final,
- their transitions have the same labels and lead to equivalent states.
Thanks to post-order method all the already processed states are minimized and unique, so equivalent states will just be the states represented by the same objects. Here’s the new key method:
def key_obj(state):
l = [state.final]
for k, v in sorted(state.transitions.items(), key=lambda x: x[0]):
l.extend([k, v.label])
return tuple(l)
Calling it on example automaton will produce the same minimized automaton as previous method:
Processing node: 4 (True,)
Processing node: 3 (False, 'p', 4)
Transition: p
Registering: 4 (True,)
Processing node: 2 (False, 's', 3)
Transition: s
Registering: 3 (False, 'p', 4)
Processing node: 7 (True,)
Processing node: 6 (False, 'p', 7)
Transition: p
Replacing 7 (True,) with 4 (True,)
Processing node: 5 (False, 's', 6)
Transition: s
Replacing 6 (False, 'p', 4) with 3 (False, 'p', 4)
Processing node: 1 (False, 'a', 2, 'i', 5)
Transition: a
Registering: 2 (False, 's', 3)
Transition: i
Replacing 5 (False, 's', 3) with 2 (False, 's', 3)
Processing node: 0 (False, 'w', 1)
Transition: w
Registering: 1 (False, 'a', 2, 'i', 2)
Constructing minimal automata directly
The method of constructing minimal automata by trie minimization has one big caveat - even if the resulting automaton is small the temporary trie structure might be orders of magnitude bigger. Luckily the minimization method can be used to come up with the algorithm for direct construction of minimal automata [1].
If we sort our input words and add them one at a time we can reproduce the same post-order traversal which we used in minimize_automata method. The only states subject to change when adding a new word, are states tied to the previous word as it may share a prefix with a new word. After finding such a common prefix, and last common state, we:
- can minimize the remaining suffix of the previous word, as we won’t modify these states anymore,
- append the suffix of the new word to the last common state.
Thanks to this approach we only keep in the memory the minimized automaton and the states belonging to the last added word.
In order to have fast access to the last added transition we will modify slightly our automaton. We will make our transitions attribute an OrderedDict instance:
def __init__(self, label):
...
self.transitions = OrderedDict()
...
and add a method to get the last added transition:
def last_transition(self):
k = next(reversed(self.transitions), None)
if k is not None:
return k, self.transitions[k]
else:
return None
Finally, here’s the implementation of the algorithm:
def minimal_automaton_from_words(words):
register = Register(key_obj)
labels = inf_labels()
start_state = State(next(labels))
for word in words:
last_state, pref_idx = common_prefix(start_state, word)
if last_state.transitions:
replace_or_register(last_state, register)
add_suffix(last_state, word[pref_idx:], labels)
replace_or_register(start_state, register)
return start_state, register
And here’s the method which registers or replaces the states from last added word:
def replace_or_register(state, register):
last_c, last_child = state.last_transition()
if last_child.transitions:
replace_or_register(last_child, register)
eq_state = register.get(last_child)
if eq_state is None:
register.put(last_child)
else:
state.add_transition(last_c, = eq_state)
Ending notes
The presented implementation is just a toy to show some ideas and not even remotely ready for any production use. It requires sorting of the input which is not always convenient. It is rather wasteful when it comes to the memory used for the representation of the states and transitions and also quite slow, partially because it’s pure Python implementation. There’s still much to be improved and maybe some of this will be addressed in the future posts. If you want to check out a good implementation of finite-state automaton check this great library: https://github.com/BurntSushi/fst. All the credits for the algorithm go to the Daciuk et al [1] whose work I heavily used when writing this post.